Kui ma vaatan tagasi viimase poole aasta jooksul tehtud töödele veebiarendajana, siis võin julgelt väita, et koolis õpitud matemaatikat kasutan ma peaaegu iga päev. Olgu selleks siis mõne veebipõhise kalkulaatori loomine, animatsioonid, elementide paigutamine või siis lihtsalt töödele hinnangute andmine.
Toon siin artiklis välja mõned põnevad matemaatika ja veebiarendaja igapäevatöö vahelised seosed.
1. Aritmeetika
Kõige lihtsamad liitmise, lahutamise, korrutamise ja jagamisega seotud tegevused on ilmselt need matemaatika osad, mida ma oma töös kõige rohkem kasutan. Kui võtame näiteks tavalise e-poe, siis aritmeetikaga puutume kokku peaaegu igas vaates.
Näiteks kui kasutaja soovib vaadata tooteid ainult kindla hinnaskaala piires, näiteks 50€ kuni 100€, siis selleks peame kasutama aritmeetilisi võrdlusoperatsioone nagu “>=” ja “<=”, et otsustada, milline toode jääb soovitud vahemikku ja milline mitte ning seejärel tulemused kasutajale välja kuvada.
Kui kasutajale on vaja pakkuda filtrit, mis võimaldab neil otsida tooteid, mille allahindlusprotsent on teatud vahemikus, siis kasutame selleks samuti aritmeetilist tehet. Iga toote allahindlusprotsendi leidmiseks peame esmalt võrdlema tooteid järgmise valemiga:

ning seejärel saame kasutajale juba soovitud tulemused kuvada.
Muidugi kasutame aritmeetilisi tehteid ka e-poe ostukorvi summade, maksude, lojaalsuspunktide, varude ja muu sellise arvutamisel.
Lisaks on aritmeetika kasutusel mitmesuguste erinevate kalkulaatorite loomisel, olgu selleks siis toote lõpphinna kalkulaator või mõni spetsiifiline laenukalkulaator. Lõpptulemuse saavutamiseks tuleb alati teha liitmist, lahutamist, korrutamist ja jagamist.
2. Mõõtühikud
Mõõtühikud, millega igapäevaselt kokku puutun, on peamiselt pikslid (px), em, rem, viewporti laius (vw) ja viewporti kõrgus (vh). Need ühikud peaks olema tuttavad kõigile, kes on kunagi kodulehte arendanud või erinevate disainitöödega tegelenud.
Piksel (px) on kõige levinum mõõtühik veebikujunduses. Tegemist on staatilise mõõtühikuga, mille abil saan täpseid suuruseid määrata. Em ja rem on suhtelised mõõtühikud, mis põhinevad vaikimisi fondi suurusel. Em viitab ülemise elemendi fondi suurusele ja rem viitab juurelemendi fondi suurusele. Neid mõõtühikud kasutades, pead sa tegelema ka aritmeetiliste tehetega.
Viewporti laius (vw) ja kõrgus (vh) on proportsionaalsed mõõtühikud, mis võimaldavad elementidel muutuda vastavalt kasutaja vaateala suurusele. Toon näite: kui määrata elemendi laiuseks 50vw, siis see hõlmab poolt kasutaja ekraani laiusest, sõltumata ekraani tegelikust suurusest.
3. Proportsioonid ja protsendiarvutus
“Kui räägime veebilehe elementide paigutusest, siis muutub väga oluliseks mõiste nimega flexbox. See on CSS (Cascading Style Sheets) meetod, mis aitab veebiarendajatel ja disaineritel lehekülje elemente paigutada nii, et veebileht näeb hea välja igas suuruses ekraanil. Aga kuidas on flexbox seotud matemaatikaga? Peamiselt läbi arvutuste, mis määravad, kuidas ja kui palju ruumi iga element lehel võtab.
Kujutlege flexboxi kui nähtamatut konteinerit, mis hoiab endas teatud elemente nagu nuppe, pilte või tekstilõike. Flexbox võimaldab meil öelda, et üks element võiks võtta rohkem ruumi kui teine või et kuidas elemendid peaksid kohanduma, kui lehe suurus muutub. Näiteks kui soovime, et üks nupp oleks teisest kaks korda laiem, siis kasutame omadusi nagu flex-grow, et seda suhet määrata.
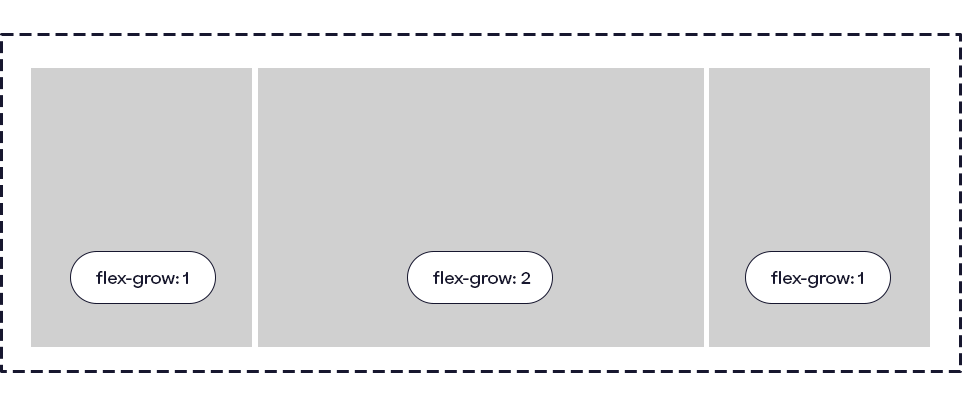
Flexbox kasutab lihtsaid aritmeetilisi suhteid, et jagada vaba ruum elementide vahel proportsionaalselt. Toome näite. Kui meil on kaks elementi ja me tahame, et üks oleks teisest kaks korda laiem, siis võime kasutada flex-grow väärtusi 2 ja 1. See tähendab matemaatilises mõttes, et esimene element võtab saadaolevast ruumist kaks kolmandikku ja teine ühe kolmandiku. Matemaatiliselt võib seda mõista järgmiselt. Kui flex-grow väärtused on 2 ja 1, siis summaarne “kasvufaktor” on kolm (kaks + üks). See tähendab, et esimene element võtab 2/3 (ehk umbes 66.67%) saadaolevast lisaruumist ja teine element 1/3 (ehk umbes 33.33%). Kui konteineri laius suureneb, siis jaotub lisaruum kahe elemendi vahel proportsionaalselt nende flex-grow väärtustega.
4. Geomeetria
Lisaks flexbox’ile kasutan ma igapäevaselt väga palju CSS animatsiooni funktsioone. Peamiselt selleks, et rippmenüüd ilmuksid sujuvalt ja nuppude hover efektid näeksid ilusad välja. Üldiselt kirjutan need välja ühe lühikese koodireaga, kuid iga vaikimisi seadistatud ajastamisfunktsioon (nagu linear, ease, ease-in, ease-out, ease-in-out) on defineeritud spetsiifiliste kuupiliste Bezier’i kõverate abil, mis määravad, kuidas animatsiooni kiirus varieerub selle kestel.
- Linear. Loob ühtlase animatsiooni ilma kiirenduse või aeglustuseta. Bezier’i kõvera mõttes tähendab see sirgjoont. Cubic Bezier’i funktsiooni parameetrid sellele on (0, 0, 1, 1).
- Ease. See vaikimisi ajastamisfunktsioon annab animatsioonile kerge alguse ja lõpu kiirenduse ja muudab liikumise loomulikumaks. Selle Bezier’i kõvera parameetrid on (0.25, 0.1, 0.25, 1).
- Ease-in. Selle funktsiooniga algab animatsioon aeglaselt ja kiireneb järk-järgult lõpuni. See simuleerib objekti “käivitumist”. Bezier’i kõvera parameetrid on (0.42, 0, 1, 1).
- Ease-out. Vastupidiselt ease-in’ile algab ease-out kiiresti ja aeglustub animatsiooni lõpu poole, simuleerides objekti “peatumist”. Bezier’i kõvera parameetrid on (0, 0, 0.58, 1).
- Ease-in-out. See funktsioon ühendab ease-in ja ease-out, alates ja lõppedes aeglaselt, kuid kiirenedes keskel. See on kasulik sujuvate ja loomulike üleminekute jaoks. Bezier’i kõvera parameetrid on (0.42, 0, 0.58, 1).
Bezier’i kõverad leiutas prantsuse insener Pierre Bezier ning nendega puutume me igapäevaselt kokku. Olgu selleks siis animatsioon või lihtsalt kenasti kujundatud teksti font. Bezier’i kõverate aluseks on kontrollpunktid. Neid kõveraid kirjeldatakse tavaliselt vähemalt kolme punktiga: alguspunkt, lõpp-punkt ja üks või mitu kontrollpunkti.
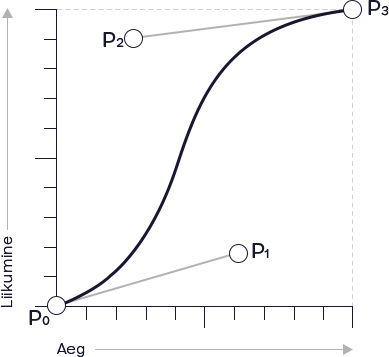
Kõvera joonistamisel arvutatakse punktide vahelised suhted, luues sujuva trajektoori, mis algab alguspunktist ja lõpeb lõpp-punktis, paindudes samal ajal kontrollpunktide suunas. Kontrollpunktid on nagu magnetid ekraanil – need ei pruugi olla joone osad, kuid nende lähedus ja asukoht mõjutavad joone kaart.
5. Võrrandid
Veebiprogrammeerija töös tuleb loomulikult ette ka võrrandite kasutamist. Oskan siin näitena tuua saatmiskulude arvutamise, kus lõpphind sõltub paki kaalust ja sihtkoha kaugusest.
Saatmiskulude arvutamiseks võime kasutada järgmist lihtsustatud mudelit:
- Baashind: Iga saadetise eest on fikseeritud baashind, näiteks 5 eurot.
- Kaalutasu: Kaalutasu on näiteks 0.5 eurot iga kaaluühiku (kg) kohta.
- Kaugustasu: Kaugustasu on näiteks 0.2 eurot iga kilomeetri kohta.
Oletame, et paki kaal on 10 kg ja sihtkoht asub 100 km kaugusel. Sel juhul saame arvutada lõpphinna kasutades järgmist valemit:

Oletame, et paki kaal on 10 kg ja sihtkoht asub 100 km kaugusel. Sel juhul saame arvutada lõpphinna. Võrrandi lahendamine annab meile vastuseks 30 eurot.
6. Statistika
Statistika on matemaatika haru, mis tegeleb andmete kogumise, korraldamise, analüüsimise ja esitamisega. Kui mul on vaja ehitada näiteks toodete soovitussüsteemi ostukorvi lehel, mis pakub klientidele tooteid nende varasema ostuajaloo ja sirvimiskäitumise põhjal, pean ma kasutama statistilist meetodit, nimega klasterdamine.
Kui ma soovin A/B testida e-poe visuaalsete erinevuste tõhusust (näiteks erinev paigutus ja reklaamsõnumid), siis kasutan ma statistikat, et teha kindlaks, kas täheldatud erinevused konversioonimäärades on juhuslikud või statistiliselt olulised. Siin tulevad mängu tõenäosusteooria ja hüpoteeside testimise meetodid.
7. Lineaaralgebra
Lineaaralgebra ja CSS-i vahel on üsna otsene seos. Eriti kui tegemist on interaktiivsete elementidega. CSS abil määratakse ära veebilehe visuaalne stiil, paigutus, värvid ja kirjatüübid. Lineaaralgebra kontseptsioonid, nagu vektorid ja maatriksid, on olulised graafiliste teisenduste ja animatsioonide loomisel, mida saab CSS-i kaudu rakendada.
CSS-i on sisse ehitatud transform omadus, et liigutada, keerata ja kallutada erinevaid elemente. Need tegevused põhinevad lineearalgebra kontseptsioonidel. Näiteks keerates veebilehel ühte kindlat elementi, kasutatakse pöörlemismaatriksit. Isegi kui minul on vaja selleks üksnes “transform: rotate(90deg)” kirjutada, siis taustal tegeleb veebibrauser siiski keeruliste maatriksarvutustega.
Matemaatika on midagi enamat kui lihtsalt numbrite jada või keerulised valemid. See on vundament, millele on ehitatud paljud meie igapäevaelu aspektid. Minu jaoks on tegemist praktilise tööriistaga, mis võimaldab mul luua esteetiliselt meeldivamaid ja funktsionaalsemaid veebilahendusi.
Tahad ühineda meie tiimiga? Nobeli meeskonda on oodatud üks tegus ja ambitsioonikas WordPress veebiarendaja. Pakume huvitavat tööd Eesti ühes suurimas digiagentuuris, inspireeriva meeskonna ja väljakutseid pakkuvate klientidega. Kandideeri siin!
Autor: Martin, Nobel Digitali veebiarendaja










